Důkazy Pythagorovy věty

Grafický důkaz Pythagorovy věty zaslaný doc. Míkou.

Pravoúhlý trojúhelník (bílá barva) a jeho tři kopie můžeme uspořádat do tvaru čtverce o straně odpovídající součtu odvěsen. Modře vybarvený čtverec uvnitř má obsah čtverce nad přeponou.

Důvtipným přeskupením jednotlivých obrazců dostaneme následující obrázek:

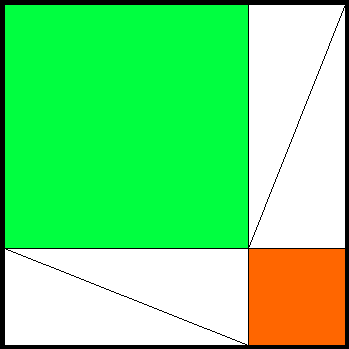
Velikost strany velkého čtverce se nezměnila - součet velikostí odvěsen trojúhelníku. Počet ani velikost pravoúhlých trojúhelníků se také nezměnila. Zbylá plocha tedy musí být stejná, jako plocha modrého čtverce. Nyní je ale rozdělena do dvou čtverců: zelený, se stranou delší odvěsny a oranžový se stranou odvěsny kratší. Jejich součet je roven čtverci nad přeponou.

2.Důkaz

Pythagorova věta říká, že součet ploch čverců nad odvěsnami je roven ploše čtverce nad základnou. Pokusme se tedy do tohoto velkého čtverce veskládat nějaké obrazce se známou plochou. Uvidíme, k čemu dojdeme.

Jediný obrazec se zatím známou plochou je vlastně sám trojúhelník a vejde se tam hned 4x.

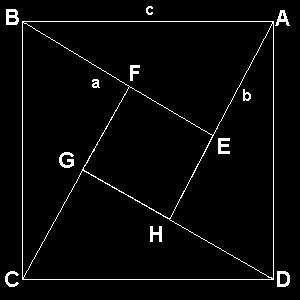
Ještě neznáme obsah čtverce EFGH uprostřed. Přesto však už teď můžeme odvodit Pythagorovu větu. A to hned dvojím způsobem:

1. matematicky

Strana čtverce EFGH má velikost rozdílu obou odvěsen "a" a "b". Jeho obsah je tedy (a-b)2. Obsah čtyř trojúhelníků je 4x(1/2ab). Obsah čtverce ABCD je tedy (a-b)2 + 4x(1/2ab) = a2 - 2ab + b2 + 2ab = a2 + b2. Protože je strana čtverce ABCD také c2, můžeme směle napsat finální formuli: c2 = a2 + b2

2. geometricky

Otočme trojúhelník CDG kolem bodu "C" tak, aby jeho přepona splynula s přeponou trojúhelníka BCF. Podobně si počínejme s trojúhelníkem DAH. Otočíme ho kolem bodu "A" a jeho přepona splyne s přeponou trojúhelníku BEA. Je na prvý pohled zřejmé, že vzniklý pravoúhlý útvar je vlastně složený ze dvou čtverců. Jeden má stranu o velikosti "a" a druhý o velikosti "b", čímž jsme vlastně naplnili naší původní ideu. Čtverec nad přeponou jsme bezezbytku vyplnili čtverci nad odvěsnami. Viz obrázek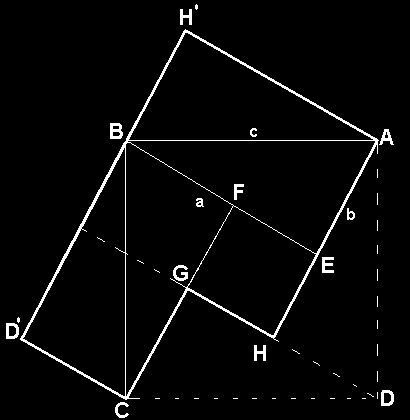

3.Důkaz

Grafický důkaz Pythagorovy věty podle Jana Nesměráka.

Je třeba dokázat, že:
Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníka se rovná součtu obsahů čtverců sestrojených nad oběma odvěsnami.

Postup:

Nad základním trojúhelníkem (zelený číslo 2) sestrojíme čtverec nad přeponou (šedivý) a oba čtverce nad (tedy lépe řečeno pod a vedle) oběma odvěsnami. Tento obrazec uzavřeme do obdélníku (vyznačen silnější bílou čarou) a rodělíme zbylé plochy na stejné trojúhelníky (budou úplně shodné jako základní trojúhelník).

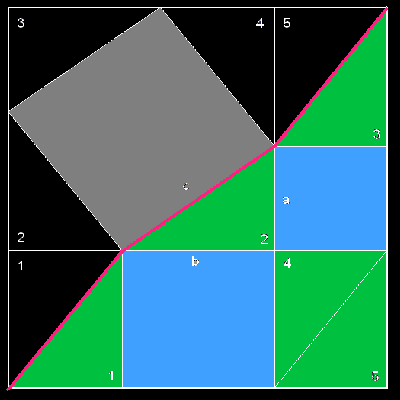
Důkaz:

Červená lomená čára nyní rozděluje obdélník na dvě stejně velké části (černo-šedou a modro-zelenou). Černo-šedá plocha obsahuje 5 trojúhelníků a čtverec nad přeponou, modro-zelená plocha obsahuje 5 trojúhelníků a čtverce nad oběma odvěsnami. Protože plocha 5-ti trojúhelníků v obou částech je nepochybně stejně velká, lze konstatovat, že obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníka se rovná součtu obsahů čtverců sestrojených nad oběma odvěsnami.

Vyjádřeno rovnicemi:
R1: [Černo-šedá plocha] = [Modro-zelená plocha]
R2: [Černo-šedá plocha] = 5 * [černý trojúhelník] + [čtverec nad přeponou]
R3: [Modro-zelená plocha] = 5 * [zelený trojúhelník] + [čtverce nad oběma odvěsnami]
R4: [černý trojúhelník] = [zelený trojúhelník]

Dosazením R4 do R2 a následně R2 a R3 do R1:

5 * [zelený trojúhelník] + [čtverec nad přeponou] = 5 * [zelený trojúhelník] + [čtverce nad oběma odvěsnami]

Q.E.D.

4.Důkaz

Nakresleme si nejprve pravoúhlý trojúhelník ABC o obsahu P.

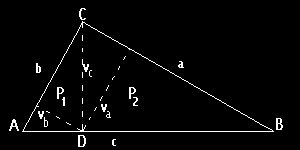
Výška v_c dělí trojúhelník na dva menší ADC a DBC s obsahy P₁ a P₂. Je zřejmé, že všechny tři dosud jmenované trojúhelníky jsou podobné, protože mají shodné úhly. Navíc je zřejmé, že

pro obsahy jednotlivých trojúhelníků platí:

II:  P=c*v_c/2
III:  P1=b*v_b/2
IV:  P2=a*v_a/2

Protože se jedná o podobné trojúhelníky, jsou poměry odpovídajících si stran (či výšek) konstantní a platí

1=b²*k/2
IV':  P2=a²*k/2

Pak ovšem platí (z rovnice I)

I':  c²*k/2=a²*k/2+b²*k/2
a po vydělení rovnice členem k/2: c²=a²+b²

5.Důkaz

Tento postup není moc elegantní. Je to takový důkaz "hrubou silou". Podívejme se na něj:

Již ve druhém důkazu jsme si ukázali, podobnost trojúhelníků ABC, ADC a DBC. Protože v podobných trojúhelnících jsou poměry odpovídajících si stran stejné, můžeme si napsat tyto rovnice:

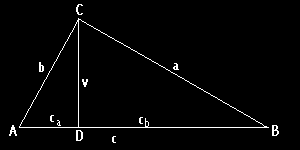
I:  c_a/b=b/c ==> b²=c*c_a
II:  c_b/a=a/c ==> a²=c*c_b


Sečteme-li obě rovnice, dostaneme:
I+II:  a²+b²=c*c_b+c*c_a
III:  a²+b²=c*(c_b+c_a)
Z obrázku je zároveň zřejmé, že: IV:  c_b+c_a=c
Pak již stačí dosadit IV do III a dostaneme

c²=a²+b²